1943. Bridges
The
undirected graph is given. Find all its bridges.
Input. The first line contains two
positive integers n and m (2 * 104, m ≤ 2 * 105) – the
number of vertices and edges in a graph respectively. Each of the next m lines contains the description of one
edge. The edge number i is described
with two positive integers bi,
ei (1 ≤ bi, ei ≤ n)
– the numbers of the vertices it connects.
Output. Print in
the first line the number b of
bridges in a given graph. Print on the next line b integers – the edge numbers that are bridges, in increasing
order. The edges are numbered from one in the order they are given at the
input.
|
Sample input |
Sample output |
6 71 22 33 41 34 54 65 6 |
1 3 |
SOLUTION
graphs – bridges
Algorithm analysis
Start the depth first search, place the d[v] and up[v] labels. There is a back edge from a vertex v or its descendant to its ancestor if and only if there is
a son to such that up[to] < d[v]. If for
some tree edge (v, to) the equality up[to]
= d[v] holds, then in the dfs subtree with the vertex v there is a back edge that comes exactly at v. If up[to] > d[v], then the
edge (v, to) is a bridge. Any back edge can’t be a bridge.
Example
Graph, given in a sample, has the
form:
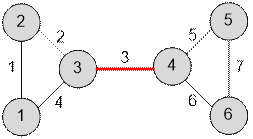
Algorithm realization
Since the number
of vertices in the graph is large, we’ll store the graph as an adjacency list graph. The array used is used to mark the already visited vertices. To
solve the problem, we’ll use
two additional arrays d and up. In the set of Bridges, we’ll collect the numbers of the edges that are bridges. For
each input edge (a, b), remember its number in the mapping mp.
vector<vector<int> > graph;
vector<int>
used, d, up;
set<int>
Bridges;
map<pair<int,int>, int> mp;
Function Edge returnes the edge, the pair of vertices (a, b),
where a < b.
pair<int,int> Edge(int a, int b)
{
if (a > b)
swap(a,b);
return
make_pair(a,b);
}
Function dfs
runs depth first search from the vertex v. Place the labels d[v] and up[v]. The
vertex p is the ancestor
of v in the search
tree.
void dfs (int
v, int p = -1)
{
used[v] = 1;
d[v] = up[v] = time++;
for (int i = 0; i < graph[v].size(); i++)
{
int to =
graph[v][i];
if (to ==
p) continue;
if
(used[to])
up[v] = min (up[v], d[to]);
else
{
dfs (to, v);
up[v] = min (up[v], up[to]);
if
(up[to] > d[v]) Bridges.insert(mp[Edge(v,to)]);
}
}
}
Function FindBridges finds the
bridges.
void FindBridges(void)
{
time = 1;
for(int i = 1; i <= n; i++)
if
(!used[i]) dfs(i);
}
The main part of the program. Read the input graph. For each edge (a, b) store its number in
the mapping mp. We need this so that
we can print the bridges not as pairs of vertices
they connect, but as the numbers of the input edges.
scanf("%d %d",&n,&m);
graph.resize(n+1);
used.resize(n+1);
d.resize(n+1);
up.resize(n+1);
for(i = 1; i <= m; i++)
{
scanf("%d
%d",&a,&b);
graph[a].push_back(b); graph[b].push_back(a);
mp[Edge(a,b)] = i;
}
Find the bridges. The
numbers of the edges that are bridges are stored in the set Bridges.
FindBridges();
Print the number of
bridges. On the next line print the numbers of the edges that are bridges in ascending order.
printf("%d\n",Bridges.size());
for(iter = Bridges.begin(); iter !=
Bridges.end(); iter++)
printf("%d ",*iter);
printf("\n");